Scale dependence of electrostatic and magnetostatic properties is investigated in the setting of spatially random linear lossless materials with statistically homogeneous and spatially ergodic random microstructures. First, from the Hill-Mandel homogenization conditions adapted to electric and magnetic fields, uniform boundary conditions are formulated for a statistical volume element (SVE). From these conditions, there follow upper and lower mesoscale bounds on the macroscale (effective) electrical permittivity and magnetic permeability. Using computational electromagnetics methods, these bounds are obtained through numerical simulations for different composites. The simulation results demonstrate a scale-dependent trend of these bounds towards the properties of a representative volume element (RVE). This transition from SVE to RVE is described using a scaling function dependent on the mesoscale δ, the volume fraction vf, and the property contrast k between two phases. The scaling function is calibrated through fitting the data obtained from extensive simulations conducted over the aforementioned parameter space. The RVE size of a given microstructure can be estimated down to within any desired accuracy using this scaling function as parametrized by the contrast and the volume fraction of different phases.

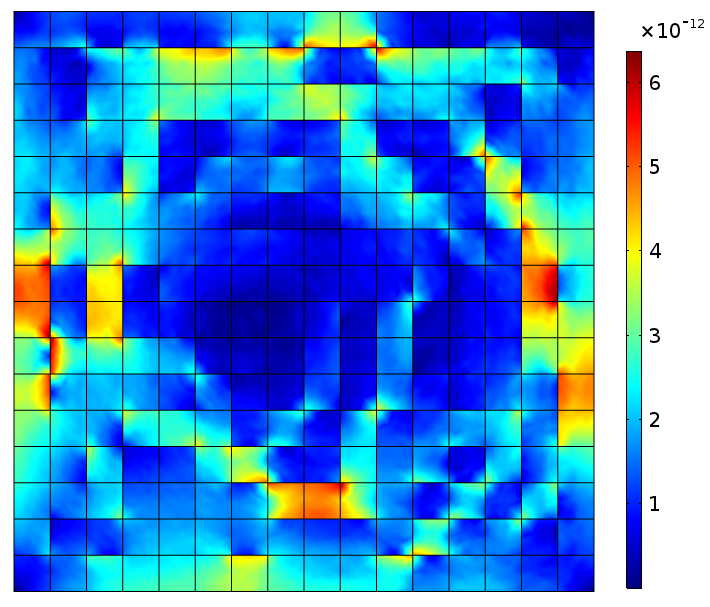
(a) Realization of a two phase random checkerboard for L = 16. (b) Magnetic flux norm density (T). (c) Magnetic field norm (A/m).

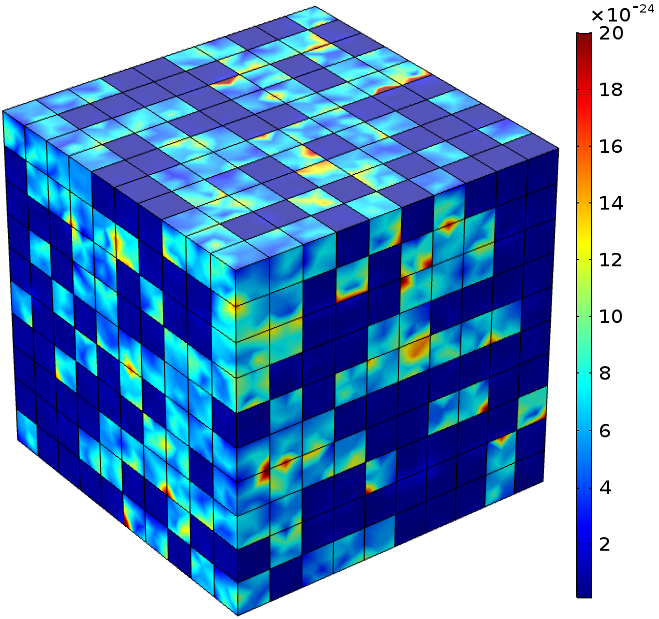
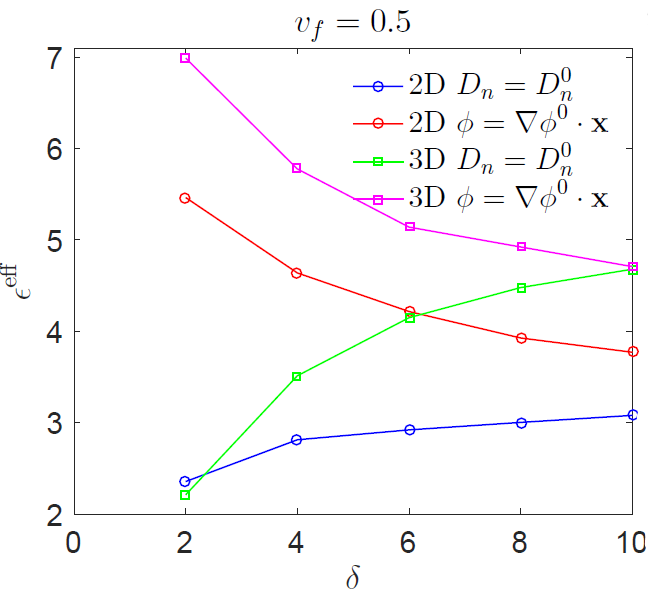
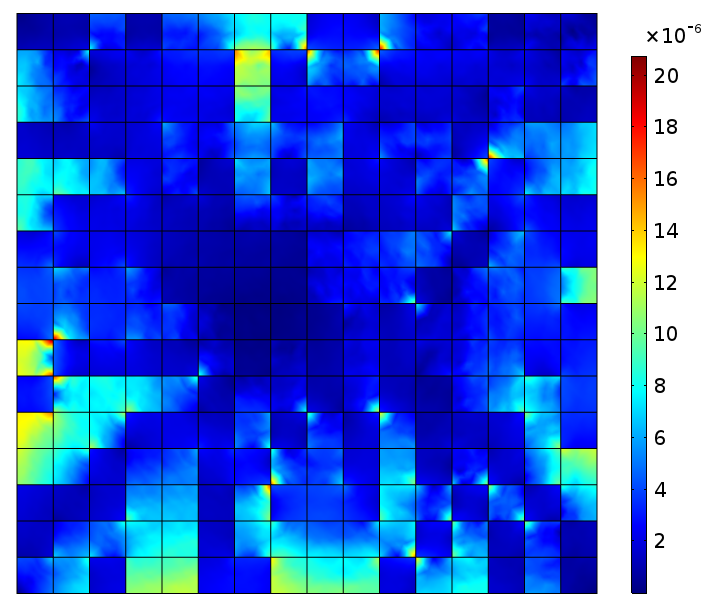
(d) 3D two-phase random checkerboard on the L x L x L lattices with L = 10. (e) Electric flux density norm (C/m^2) for 3D two-phase random checkerboard. (f) Comparison of scaling effects for vf = 0.5 in 2D and 3D random two phase checkerboard.
P. Karimi, X. Zhang, S. Yan, M. Ostoja-Starzewski, and J. M. Jin, “Electrostatic and magnetostatic properties of random materials," Phys. Rev. E, accepted for publication, February 2019.
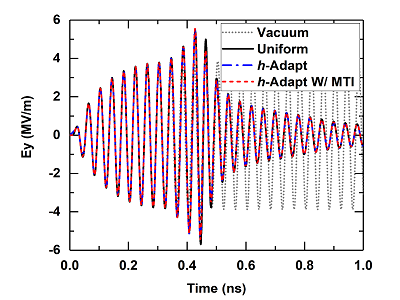
Interactions between electromagnetic (EM) fields and plasma lead to many interesting physical phenomena, including high-power microwave air breakdown, plasma shielding effect, and plasma streamer discharge. The physically competing ionization-diffusion mechanism usually results in a abrupt change of the plasma density at the edges of plasma bulks, which requires an extremely high spatial resolution in a numerical simulation. To provide a sufficient spatial resolution while maintaining a reasonably low computational cost, it is desirable to develop a technique that can identify and refine regions requiring a higher resolution from the rest. In this project, we develop a discontinuous Galerkin time-domain (DGTD) algorithm with a dynamic h-adaption technique to handle non-conformal, time-varying, and automatically adjustable meshes. Identification procedures with different criteria are investigated for their effectiveness and robustness in the mesh refinement automation. A multirate time integration technique is employed to perform an efficient time marching by permitting different time step sizes in elements with different scales. The implementations of both the EM-plasma diffusion and the EM-five-moment plasma fluid models enable the proposed techniques to be applicable in a wide range of EM-plasma simulations.
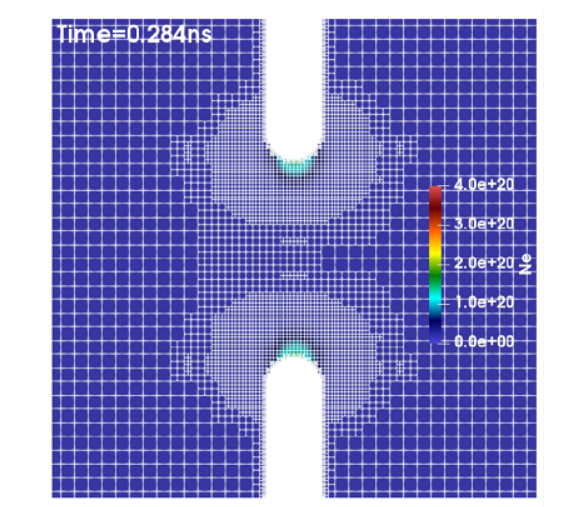
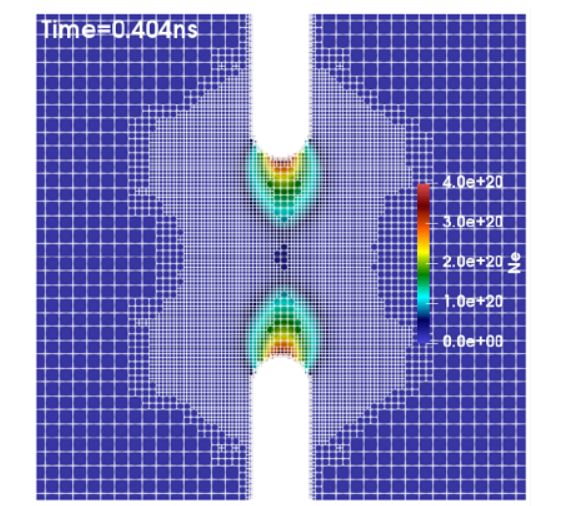
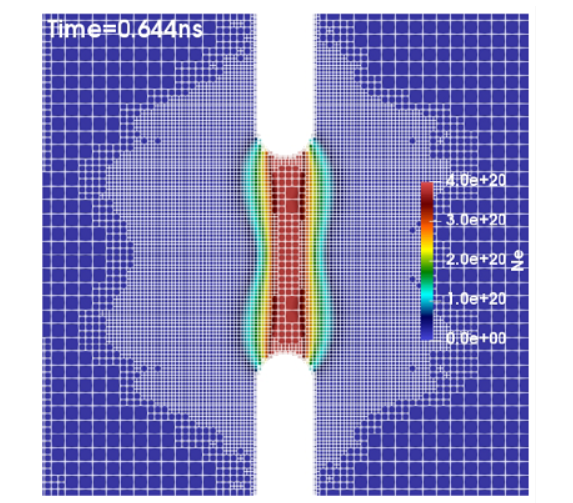
(a)-(c) Snapshots of the electron density distribution inside an air-filled aperture modeled with a dynamic mesh.
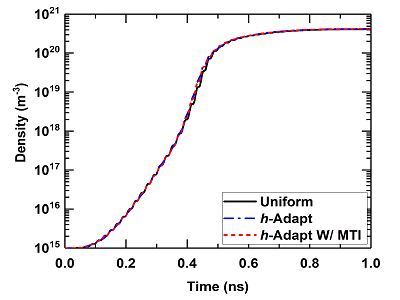
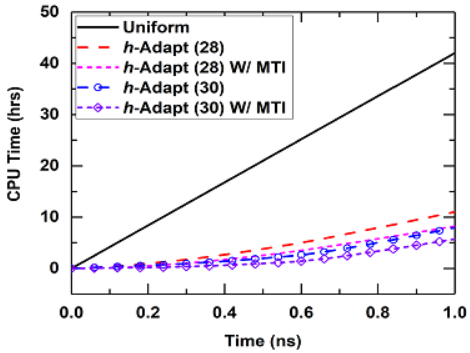
S. Yan, J. W. Qian and J.-M. Jin, “An Advanced EM–Plasma Simulator Based on the DGTD Algorithm with Dynamic Adaptation and Multirate Time Integration Techniques," IEEE Journal on Multiscale and Multiphysics Computational Techniques, submitted for review.
S. Yan, C.-P. Lin, R. R. Arslanbekov, V. I. Kolobov and J.-M. Jin, “A Discontinuous Galerkin Time-Domain Method With Dynamically Adaptive Cartesian Mesh for Computational Electromagnetics," in IEEE Transactions on Antennas and Propagation, vol. 65, no. 6, pp. 3122-3133, June 2017.
Determining the dimensions of nanostructures is distinctly vital to maximizing the performance of many geometry-sensitive functional devices, such as semiconductor integrated circuits, plasmonic biosensors, and integrated photonic devices. However, accurate metrology of nano-structures is difficult to achieve using optics-based methods due to the diffraction limit and the unavoidable measurement noise. These measurements are conventionally performed using electron-based imaging techniques such as the scanning electron microscopy (SEM) and the transmission electron microscopy (TEM). In this project, we use a deep convolutional neural network (CNN) model to retrieve the subwavelength geometrical profiles of nano-structures from single-shot diffraction-limited optical images or high-dimensional optical scattering spectra. We demonstrate the effectiveness and accuracy of our method by validations on both simulations and experiments on a NIST sample and a DRAM transistor array. Our CNN model is fast (inference within 10 milliseconds), accurate (within single-digit nanometer uncertainty), robust to noise, and non-destructive. With the help of deep learning, we aim at extending conventional optics-based metrology approaches into nanoscale.
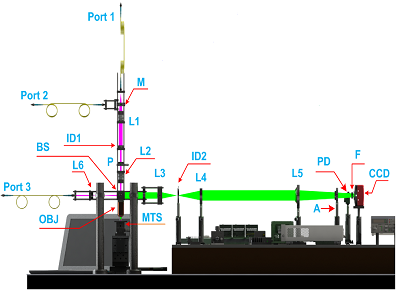

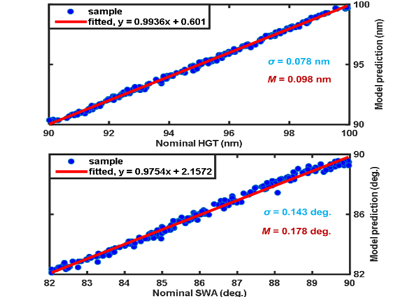
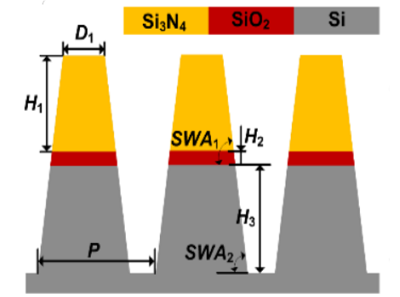
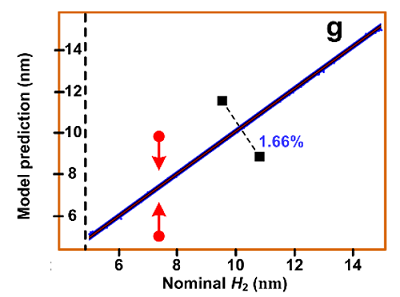
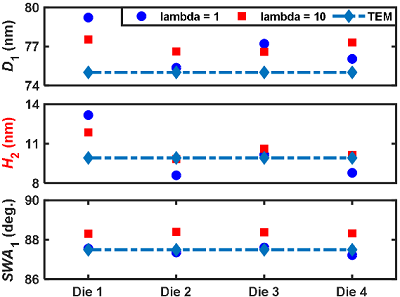
J. L. Zhu, Y. N. Liu, S. Purandare, J.-M. Jin, S. Liu, and L. Goddard, “Optical Deep Learning Nano-Profilometry," Light: Science and Applications, submitted for review.
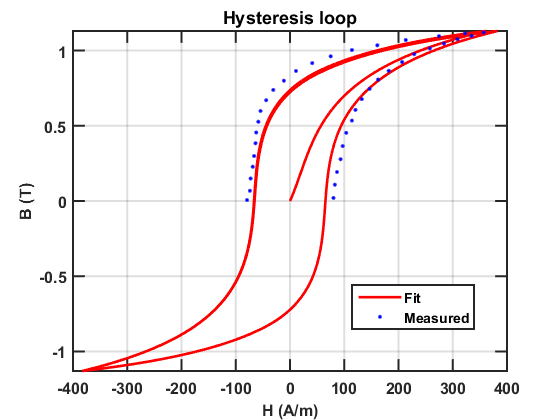
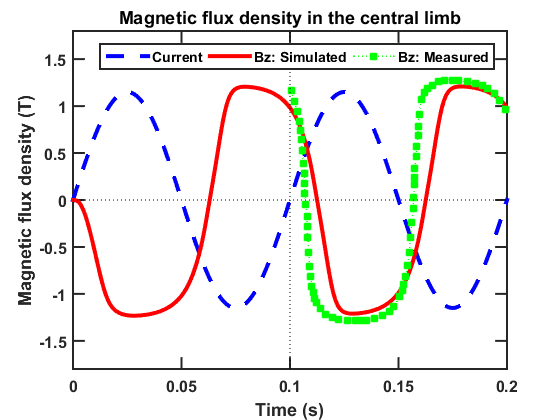
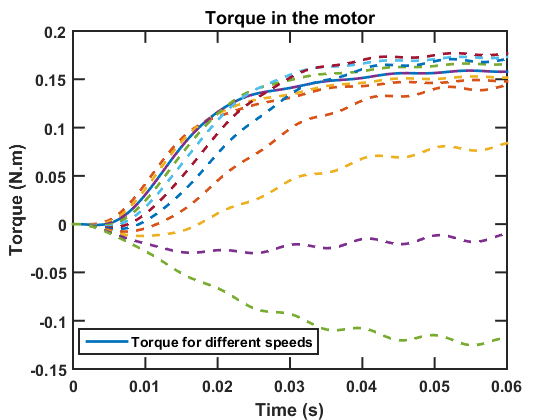
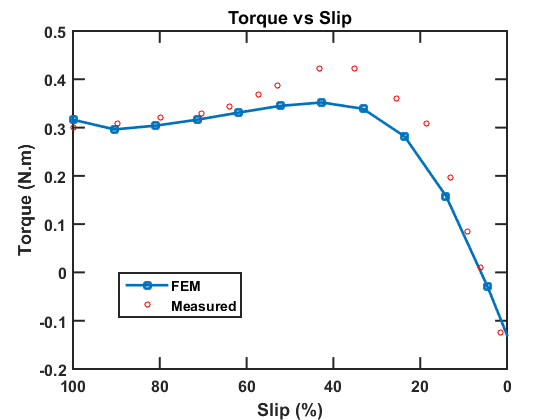
Accurate modeling is essential in the electrical machinery design in order to predict the performance. The finite element method is widely used as the primary approach to optimal design. However, there are two major challenges. In real applications, the cores are typically made of ferromagnetic materials, which exhibit hysteresis property. It is critical to take into account this nonlinear effect to achieve an accurate estimation of the efficiency. In this work, the Jiles-Atherton (J-A) model is incorporated into the time-domain finite element method (TDFEM) to simulate the nonlinear hysteresis phenomena. Besides, when the analysis of the induction motor is performed, it is desired to consider the performance versus the speed of the rotor. For different types of rotating objects, different methods are developed. When the objects are smooth along the rotating direction, the motion can be easily modeled by adding the Lorentz term. When the geometry varies during the movement, however, a more complicated method is required. In the work, a domain decomposition method is proposed, and the sliding interface is coupled using the mixed boundary condition.
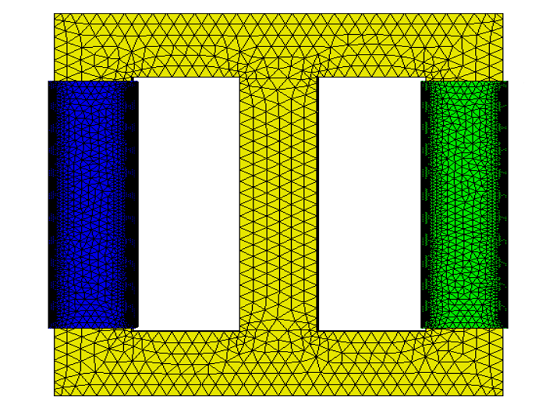

In this work, the air breakdown problem encountered with high-power microwave (HPM) operation is modeled using a fully coupled nonlinear Newton scheme in the time domain. During the air breakdown process, the HPM ionizes neutral air molecules and generates free electrons, which are pushed to move by the Lorentz force produced by the electromagnetic fields. The motion of free electrons produces plasma currents, which generate secondary electromagnetic fields that couple back to the externally applied fields and interact with the free electrons. Such a breakdown process is highly nonlinear, and can be described by a coupled electromagnetic-plasma system, where the electromagnetic fields are governed by Maxwell’s equations and the plasma current is modeled by a simplified plasma fluid equation due to the high electron density in the air breakdown under the atmosphere condition. The coupled nonlinear system equations are solved by the time-domain finite element method (TDFEM) together with a coupled Newton’s method. Numerical examples are presented to demonstrate the nonlinear characteristics of the breakdown phenomenon and the self-sustaining property of the plasma current.
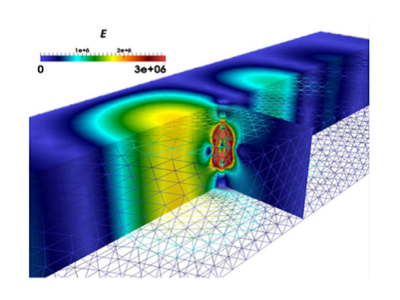
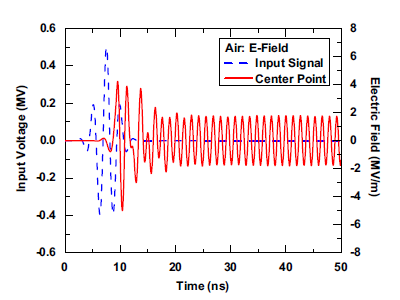
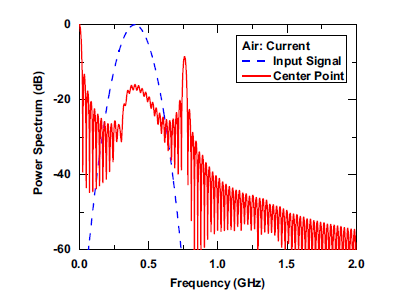
S. Yan and J.-M. Jin, “A fully coupled nonlinear scheme for time-domain modeling of high-power microwave air breakdown,” IEEE Trans. Microwave Theory Tech., vol. 64, no. 9, pp. 2718-2729, Sept. 2016.
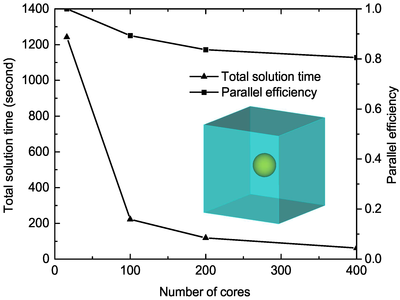
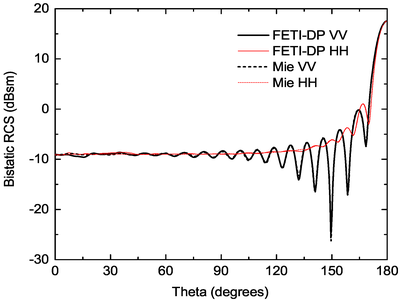
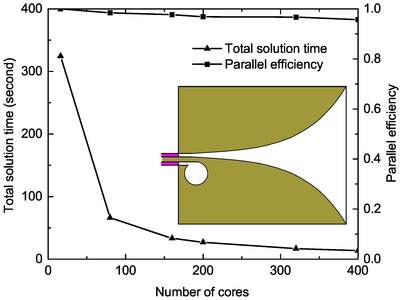
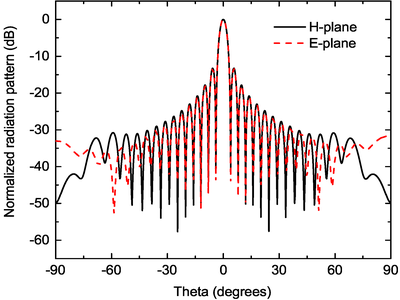
In this work, an efficient parallel strategy for the FETI-DP algorithm is proposed. To achieve a good load balance, the mesh is partitioned into subdomains with similar sizes and shapes. The subdomains in close proximity are then distributed to the same processor to minimize inter-process communication. The parallel generalized minimal residual method, enhanced with the iterative classical Gram-Schmidt orthogonalization scheme to reduce global communication, is adopted to solve the order-reduced global interface problem in the FETI-DP algorithm with a fast convergence rate. The global coarse problem, formed to improve the convergence of the global interface problem, is solved iteratively by a parallel communication-avoiding biconjugate gradient stabilized method to minimize global communication. The iterative solution of the global coarse problem is accelerated by a diagonal preconditioner constructed from the coarse system matrix. To alleviate neighboring communication overhead, the non-blocking communication approach is employed in both Krylov subspace methods. Numerical examples are presented to demonstrate the accuracy and scalability of the proposed parallel scheme for electromagnetic modeling of general objects and antenna arrays.
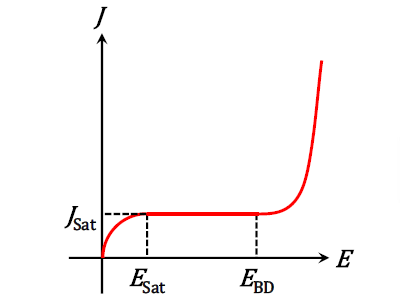
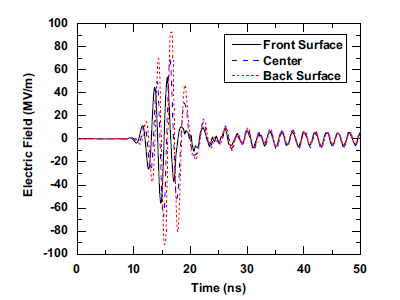
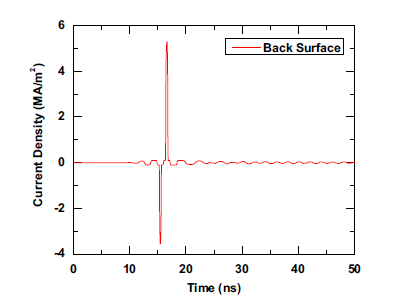
S. Yan and J.-M. Jin, “Three-dimensional time-domain finite element simulation of dielectric breakdown based on nonlinear conductivity model," IEEE Trans. Antennas Propagat., vol. 64, no. 7, pp. 3018-3026, July 2016.
The standard finite-element method (FEM) is one of the best choices for materials with complex structures. At material interfaces, the FEM has to resort to meshes that are conformal with the interfaces to yield an accurate representation of the solution. However the discretization of complex 3D objects with high quality elements remains challenging and time-consuming despite the rapid development of the computer aided design (CAD). There are also other occasions, such as crack growth simulations, shape optimizations, and transient field analysis, where the generation of multiple conformal meshes needed to capture the geometric changes is cumbersome, expensive, and sometimes impractical. In this work, an interface-enriched generalized FEM (IGFEM) is proposed for accurate and efficient electromagnetic analysis of problems involving intricate internal structures. Without using meshes that conform to the material interfaces, which greatly lessens the burden of mesh generation, the method assigns generalized degrees of freedom (DOFs) at material interfaces to capture the normal derivative discontinuity of the tangential field. The generalized DOFs are supported by enriched vector basis functions, which are constructed through a linear combination of the vector basis functions from the sub-elements. Several verification examples are provided to show that the IGFEM is not sensitive to the quality of the sub-elements and maintains the same level of solution accuracy and computational complexity as the standard FEM based on conformal meshes. The potential of the proposed IGFEM is demonstrated by simulating some engineering problems with complex, periodic internal structures, including composite materials with randomly distributed spherical particles and ellipsoidal inclusions and microvascular channels.
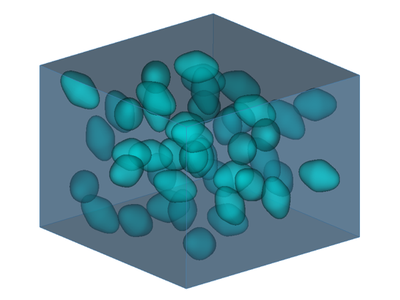
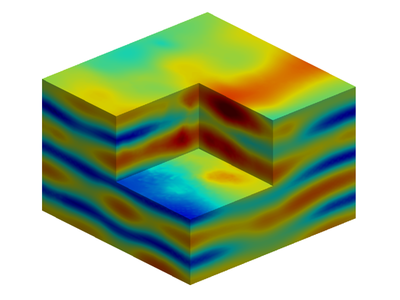
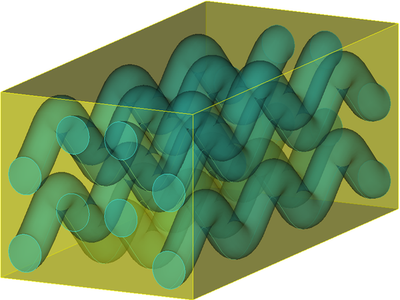
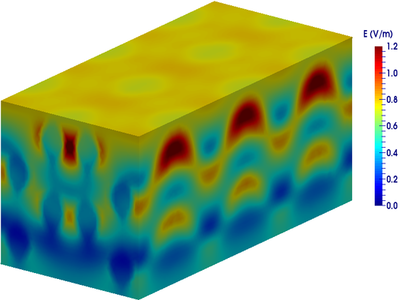
K. D. Zhang, J.-M. Jin, and P. H. Geubelle, “A 3D Interface-Enriched Generalized FEM for Electromagnetic Problems with Non-Conformal Discretizations,” IEEE Trans. Antennas Propagat., vol. 63, no. 12, pp. 5637-5649, Dec. 2015.
K. D. Zhang, A. Raeisi Najafi, J.-M. Jin, and P. H. Geubelle, “An Interface-Enriched Generalized Finite Element Analysis for Electromagnetic Problems with Non-Conformal Discretizations,” Int. J. Num. Model: Electronic Networks, Devices and Fields, vol. 29, no. 2, pp. 265-279, 2016.
The dual-primal finite-element tearing and interconnecting (FETI-DP) algorithm has been shown to be very powerful for electromagnetic analysis because of its numerical stability. As a nonoverlapping domain decomposition method, the FETI-DP algorithm forms fully decoupled subdomain problems and exhibits high scalability potential. However, due to the complex structure of this algorithm, efficient parallelization is not trivial, especially on a large number of processors. In this work, an efficient parallel strategy for the FETI-DP algorithm is proposed. To achieve a good load balance, the mesh is partitioned into subdomains with similar sizes and shapes. The subdomains in close proximity are then distributed to the same processor to minimize inter-process communication. The parallel generalized minimal residual method, enhanced with the iterative classical Gram-Schmidt orthogonalization scheme to reduce global communication, is adopted to solve the order-reduced global interface problem in the FETI-DP algorithm with a fast convergence rate. The global coarse problem, formed to improve the convergence of the global interface problem, is solved iteratively by a parallel communication-avoiding biconjugate gradient stabilized method to minimize global communication. The iterative solution of the global coarse problem is accelerated by a diagonal preconditioner constructed from the coarse system matrix. To alleviate neighboring communication overhead, the non-blocking communication approach is employed in both Krylov subspace methods. Numerical examples are presented to demonstrate the accuracy and scalability of the proposed parallel scheme for electromagnetic modeling of general objects and antenna arrays.
K. D. Zhang and J.-M. Jin, “Parallel FETI-DP Algorithm for Efficient Simulation of Large-Scale EM Problems,” Int. J. Num. Model: Electronic Networks, Devices and Fields, vol. 29, no. 5, pp. 897-914, 2016.
Nonlinear phenomena in electromagnetics generally involve changes in the material properties due to the presence of electromagnetic fields. The changes in the material properties in turn modify the state of the original electromagnetic fields in the medium. Since the material properties and the contained fields interact with each other constantly, it is most natural to describe and model these interactions in the time domain, where at each time instant the changes in the fields induce nonlinear modifications on both the material properties and the fields themselves. In this work, a discontinuous Galerkin time-domain (DGTD) algorithm is formulated and implemented to model the third-order instantaneous nonlinear effect on electromagnetic fields due the field-dependent medium permittivity. The nonlinear DGTD computation is accelerated using graphics processing units (GPUs), and examples are presented to show the different Kerr effects observed through the third-order nonlinearity. With the acceleration using MPI + GPU under a large cluster environment, the solution times for nonlinear simulations are significantly reduced.
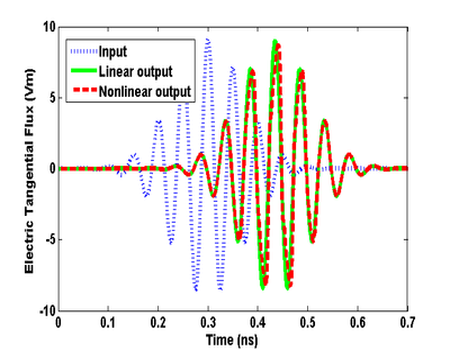
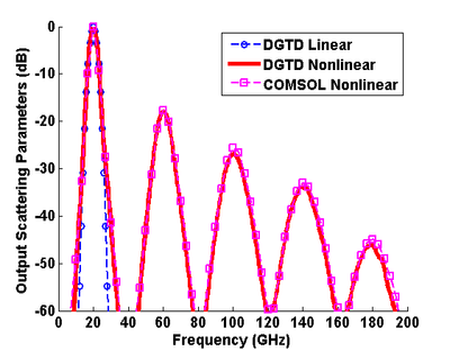
H.-T. Meng and J.-M. Jin, “GPU Acceleration of Nonlinear Modeling by the Discontinuous Galerkin Time-Domain Method,” ACES Express, vol. 1, no. 4, pp. 121-124, April 2016.
An accurate and efficient finite element-boundary integral (FE-BI) method with graphics processing unit (GPU) acceleration is presented for solving electromagnetic problems with complex structures and materials. A mixed testing scheme, in which the Rao-Wilton-Glisson and the Buffa-Christiansen functions are both employed as the testing functions, is first presented to improve the accuracy of the FE-BI method. An efficient absorbing boundary condition (ABC)-based preconditioner is then proposed to accelerate the convergence of the iterative solution. To further improve the efficiency of the total computation, a GPU-accelerated multilevel fast multipole algorithm (MLFMA) is applied to the iterative solution. The radar cross sections (RCS) of several benchmark objects are calculated to demonstrate the numerical accuracy of the solution and also to show that the proposed method not only is free of interior resonance corruption, but also has a better convergence than the conventional FE-BI methods. The capability and efficiency of the proposed method are analyzed through several numerical examples, including a large dielectric coated sphere, a partial human body, and a coated missile-like object. Compared with the 8-threaded CPU-based algorithm, the GPU-accelerated FE-BI-MLFMA algorithm can achieve a total speedup up to 25.5 times.
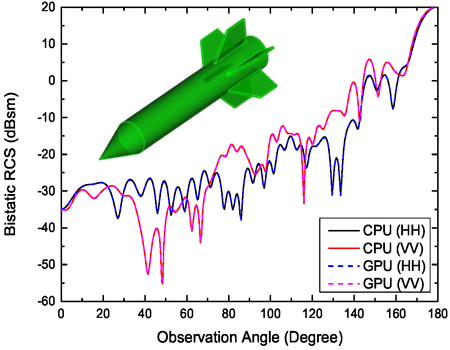
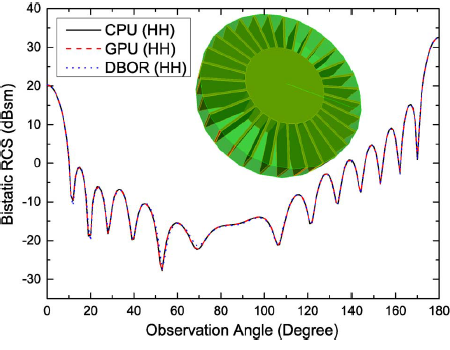
J. Guan, S. Yan, and J.-M. Jin, "An Accurate and Efficient Finite Element-Boundary Integral Method with GPU Acceleration for 3-D Electromagnetic Analysis," IEEE Trans. Antennas Propag., vol. 62, no. 12, pp. 6325-6336, Dec. 2014.
With the fast rate of innovation of portable wireless devices, more and more communication and entertainment functions are featured in portable devices such as cell phones, many of which require the integration of multiple transmitting/receiving antennas into the limited space of the device. In this research, we propose to simulate the SAR induced in the human head by multiple transmitting antennas, and the total radiated power (TRP) from the antenna into the space. In order to obtain robust mathematical models for SAR and TRP that incorporate various input parameters, we will consider different scenarios, for example, different operating frequencies, different phase combinations of the input signals, different physical locations of the antennas, and different gestures in which customer holds the device. Based on the data obtained from the full-wave simulation, we will formulate and construct accurate mathematical models for the SAR and TRP. We will check the models against different input parameter combinations for validation purposes. The result of this research serves as a starting point for the SAR minimization with the multiple transmitting chains in portable devices.
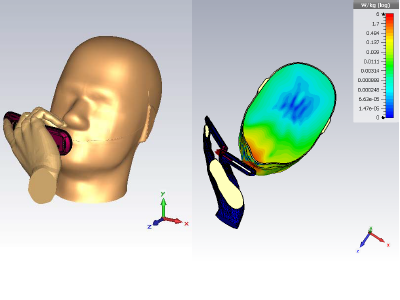
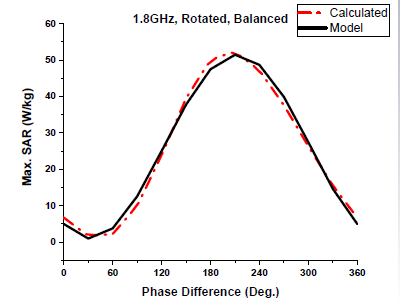
J. Li, S. Yan, Y. Liu, B. M. Hochwald, and J. M. Jin, “A high-order model for fast estimation of specific absorption rate induced by multiple transmitters in portable devices,” IEEE Trans. Antennas Propagat., vol. 65, no. 12, pp. 6768-6778, Dec. 2017.
B. M. Hochwald, D. J. Love, S. Yan, P. Fay, and J. M. Jin, “Incorporating specific absorption rate (SAR) constraints into wireless signal design,” IEEE Communications Magazine, vol. 52, no. 9, pp. 126-133, Sept. 2014.
A multi-GPU implementation of the multilevel fast multipole algorithm (MLFMA) based on the hybrid OpenMP-CUDA parallel programming model (OpenMP-CUDA-MLFMA) is presented for computing electromagnetic scattering of a three-dimensional conducting object. The proposed hierarchical parallelization strategy ensures a high computational throughput for the GPU calculation. The resulting OpenMP-based multi-GPU implementation is capable of solving real-life problems with over one million unknowns with a remarkable speed-up. The radar cross sections of a few benchmark objects are calculated to demonstrate the accuracy of the solution. The results are compared with those from the CPU-based MLFMA and measurements. The capability and efficiency of the presented method are analyzed through the examples of a sphere, an aerocraft, and a missile-like object. Compared with the 8-threaded CPU-based MLFMA, the OpenMP-CUDA-MLFMA method can achieve from 5 to 20 total speed-up ratios.
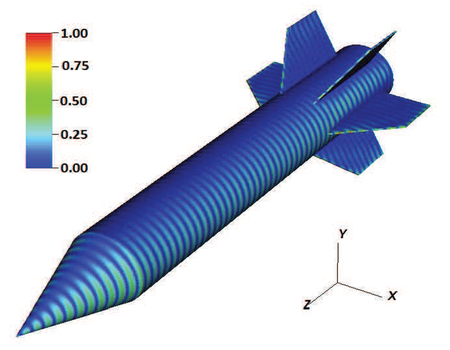
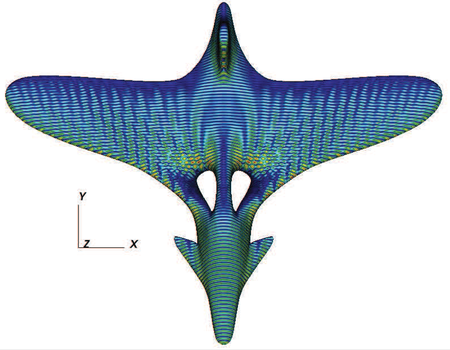
J. Guan, S. Yan, and J.-M. Jin, "An OpenMP-CUDA implementation of multilevel fast multipole algorithm for electromagnetic simulation on multi-GPU computing systems," IEEE Trans. Antennas Propag., vol. 61, no. 7, pp. 3607-3616, July, 2013.
General-purpose computing on graphics processing units (GPGPU), with programming models such as the Compute Unified Device Architecture (CUDA) by NVIDIA, offers the capability to accelerate the solution process of computational electromagnetic analysis. However, due to the communication-intensive nature of the finite element algorithm, both the assembly and the solution phases cannot be implemented via fine-grained many-core GPU processors in a straightforward manner. In this work, we identify the bottlenecks in the GPU parallelization of the finite element method for electromagnetic analysis, and propose potential solutions to alleviate the bottlenecks. We first investigate efficient parallelization strategies for the finite element matrix assembly on a single GPU and on multiple GPUs. We then explore parallelization strategies for the finite element matrix solution, in conjunction with parallelizable preconditioners to reduce the total solution time. We show that with a proper parallelization and implementation, GPUs are able to achieve significant speedup over OpenMP enabled multi-core CPUs.
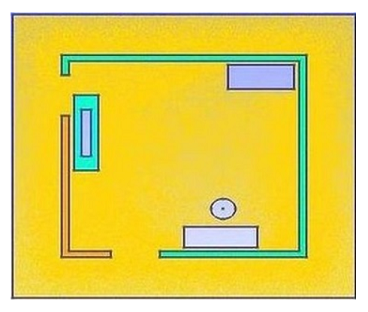
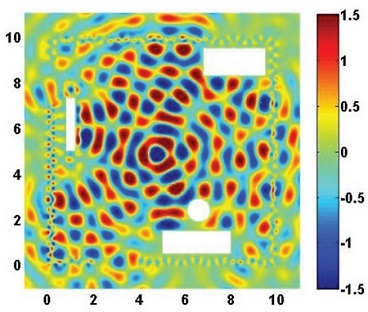
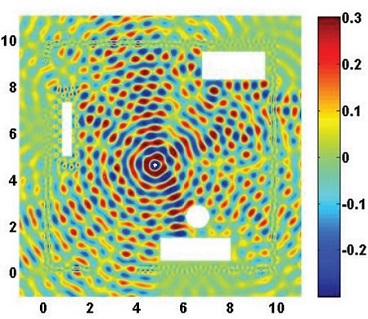
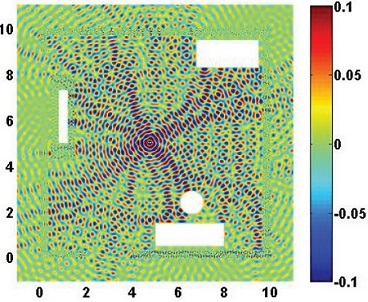
(a) Geometry of the room. Resulting field distribution at (b) 300MHz, (c) 500MHz, and (d) 1000MHz.
H.-T. Meng and J.-M. Jin, “Acceleration of the dual-field domain decomposition algorithm using MPI-CUDA on large-scale computing systems,” IEEE Trans. Antennas Propag., vol. 62, no. 9, pp. 4706-4715, Sept. 2014.
H.-T. Meng, B.-L. Nie, S. Wong, C. Macon, and J.-M. Jin, “GPU accelerated finite element computation for electromagnetic analysis,” IEEE Antennas Propag. Mag., vol. 56, no. 2, pp. 39-62, Apr. 2014.